![]()
Mise en contexte :
L’agriculture est un des stades obligatoires de la survie, pour obtenir une première source de nourriture facile, à consommer directement ou destinée à vos animaux. L’avantage de cette dernière est d’être plus facilement automatisable que l’élevage : si le cacao nécessite une intervention du joueur, la culture du melon et de la citrouille est entièrement automatisable et les villageois peuvent désormais s’occuper des cultures de blé, pommes de terre et carottes.
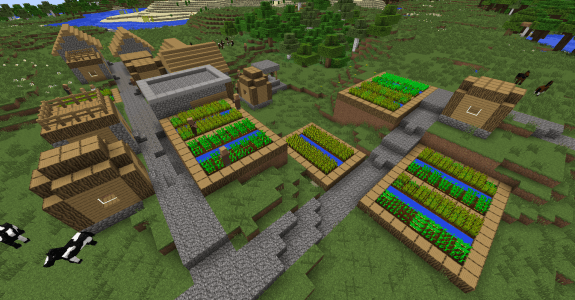 Champs de blé, de carottes et de pommes de terre entretenus par des villageois
Champs de blé, de carottes et de pommes de terre entretenus par des villageois
Certes, nos cultures sont automatisables, mais augmenter le rendement nécessite de savoir comment les plantes poussent dans le jeu. Nous allons nous intéresser à la disposition des plantes dans les champs afin de confirmer certaines techniques de joueur.
![]()
Mise en évidence du phénomène
On cherche ici à suivre l’évolution d’un champ au court du temps.
 Vue du montage expérimental
Vue du montage expérimental
Le principe est le suivant : on forme une surface de terre qu’on laboure et qu’on hydrate. On la recouvre ensuite de plantes et on suit la croissance des plantes
- Conditions de l'expérience
- Plantes étudiées et croissance
- Dispositions possibles
- Code couleur
- Première étape : capturer l'état
- Seconde étape : traiter les données
 La croissance des plantes dans le jeu, si elle ressemble un peu les plantes réelles, dépend de nombreuses variables. On s’intéresse uniquement à la disposition ici, on fixe donc les facteurs environnementaux :
La croissance des plantes dans le jeu, si elle ressemble un peu les plantes réelles, dépend de nombreuses variables. On s’intéresse uniquement à la disposition ici, on fixe donc les facteurs environnementaux :
- le cycle jour-nuit a été désactivé et l’heure est fixée vers midi :
/gamerule doDaylightCycle false
/time set 6000
- la pluie et l’orage a été désactivée :
/weather clear 1000000
- l’hydratation de la terre labourée est maximale : la zone de test est composée de 6×6 zones de 9×9 blocs hydratées par une source d’eau au centre. Il y a donc au total 2 880 blocs de terre labourée.
- la vitesse de pousse est celle du jeu par défaut :
/gamerule randomTickSpeed 3
Note : la difficulté du jeu a été mise à 0 (mode Paisible), le biome utilisée est Plaine et la zone est entièrement contenue dans la zone du chunk principal (pour que la zone de test soit constamment chargée). La version utilisée est la 1.8.9.
 Les plantes passent par différents stades de croissance. Ces stades sont représentés par une augmentation de la Data value du bloc, que nous avons déjà expliqué dans le test sur la canne à sucre. Nous étudierons trois plantes :
Les plantes passent par différents stades de croissance. Ces stades sont représentés par une augmentation de la Data value du bloc, que nous avons déjà expliqué dans le test sur la canne à sucre. Nous étudierons trois plantes :
- le blé : 8 stades de croissance, de 0 (les graines plantées) à 7 (mûr)
- la carotte : 8 stades de 0 à 7, mais il ne possède pas de visuels différents à tous les stades.
- la pomme de terre : 8 stades de 0 à 7, mais il ne possède pas de visuels différents à tous les stades.
Note : la verrue du Nether, le cacao et la betterave en version 1.9 ont seulement 4 stades de pousse.
 L’objet de l’étude concerne donc la disposition de deux plantes. On peut imaginer de nombreux cas :
L’objet de l’étude concerne donc la disposition de deux plantes. On peut imaginer de nombreux cas :
- deux parties distinctes.
- des bandes de 1 bloc de large alternées.
- un maillage alterné avec des carrés de 1 bloc.
- et toute autre disposition qui garde une répartition 50-50 de chaque plante.
Nous allons donc effectuer les mesures pour chacune des dispositions présentées, puis les comparer pour conclure.
 Lorsqu’on génère une grille, chaque item a la même coordonnée y, ce qui est l’équivalent d’un plan horizontal (en rose). Les objets qui seront absorbés sont l’intersection de la zone de récupération et de ce plan, ce qui forme une zone vide rectangulaire (représentée en rouge).
Lorsqu’on génère une grille, chaque item a la même coordonnée y, ce qui est l’équivalent d’un plan horizontal (en rose). Les objets qui seront absorbés sont l’intersection de la zone de récupération et de ce plan, ce qui forme une zone vide rectangulaire (représentée en rouge).
Donc nos expériences précédentes ne sont qu’une petite fraction de la zone de récupération, il va falloir trouver des méthodes pour balayer la dimension verticale.
 Pour laisser la zone de test intacte lors des mesures, on effectue une copie de l’état sur une autre surface à proximité. Cela permet d’avoir une image visuelle pour suivre facilement l’évolution des plantes.
Pour laisser la zone de test intacte lors des mesures, on effectue une copie de l’état sur une autre surface à proximité. Cela permet d’avoir une image visuelle pour suivre facilement l’évolution des plantes.
Pour chaque stade ![]() (de 0 à 7), on effectue la procédure suivante :
(de 0 à 7), on effectue la procédure suivante :
- on copie toutes les plantes au stade
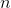 présents dans la zone de test (en rouge) dans la zone de copie (en bleu) :
présents dans la zone de test (en rouge) dans la zone de copie (en bleu) :
/clone <x1> <y1> <z1> <x2> <y2> <z2> <X1> <Y1> <Z1> filtered normal minecraft:<plante> ![]()
- on remplace les plantes copiées par un tapis de la couleur correspondant au code couleur défini précédemment :
/fill <X1> <Y1> <Z1> <X2> <Y2> <Z2> minecraft:carpet <DV> replace minecraft:<plante> ![]()
L’opération doit être faite pour chaque plante et chaque stade, ce qui correspond à 2×2×8 = 32 étapes pour nos expériences (on se limite à 2 types de plantes).
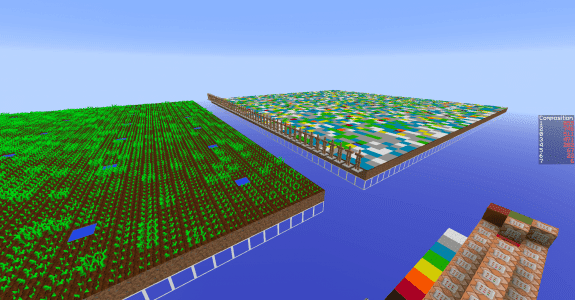 Une fois la copie effectuée, reste à l’analyser. On utilise pour cela 6×9 = 54 ArmorStands qui vont balayer horizontalement la surface. Avant de se déplacer d’une unité, l’ArmorStand détecte la couleur du tapis et ajoute au tableau des scores correspondant la valeur correspondante.
Une fois la copie effectuée, reste à l’analyser. On utilise pour cela 6×9 = 54 ArmorStands qui vont balayer horizontalement la surface. Avant de se déplacer d’une unité, l’ArmorStand détecte la couleur du tapis et ajoute au tableau des scores correspondant la valeur correspondante.
Par exemple, pour compter le nombre de plantes au stade 0, on augmente de 1 le score Composition du joueur nommé “0” à chaque fois qu’on détecte un tapis blanc :
/execute @e[type=ArmorStand] ~ ~ ~ detect ~ ~ ~ minecraft:carpet 0 /scoreboard players add 0 Composition 1
Et ceci est fait pour chacune des 8 couleurs de tapis. Lorsqu’on a fini une zone, il faut réinitialiser les scores de ces joueurs “virtuels”. La méthode utilisée est de supprimer puis de recréer l’objectif “Composition” :
/scoreboard objectives remove Composition
/scoreboard objectives add Composition dummy
/scoreboard objectives setdisplay sidebar Composition
La dernière ligne de commande sert à remettre l’affichage des scores sur la partie droite, c’est purement esthétique.
Maintenant que nous avons les outils, il ne reste plus qu’à faire les mesures !
![]()
Résultats préliminaires :
Avant de développer la théorie concernant un phénomène, il est préférable de montrer que ce phénomène existe. De nombreuses comparaisons de dispositions des plantes dans les cultures ont été souvent produites, la plus connue étant la vidéo Minecraft MythBusting de xisumavoid, ce premier montage permet d’illustrer visuellement et numériquement le phénomène.
 Croissance accélérée d’un champ (plantation en deux blocs distincts)
Croissance accélérée d’un champ (plantation en deux blocs distincts)
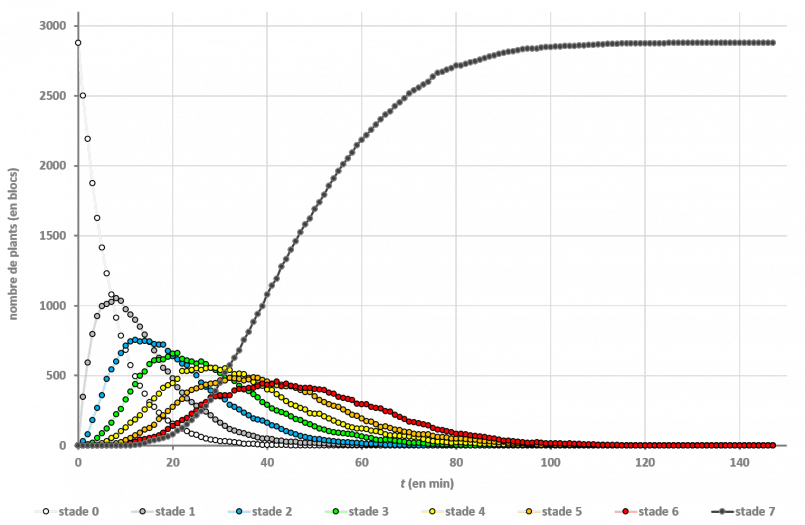
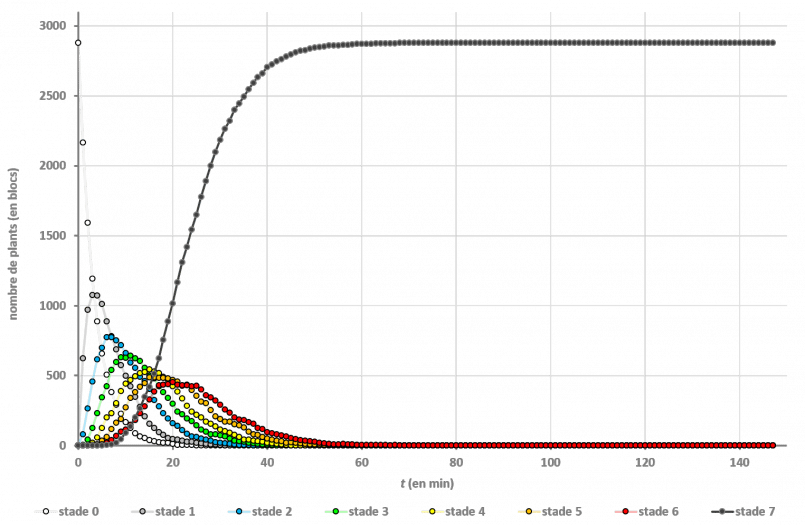
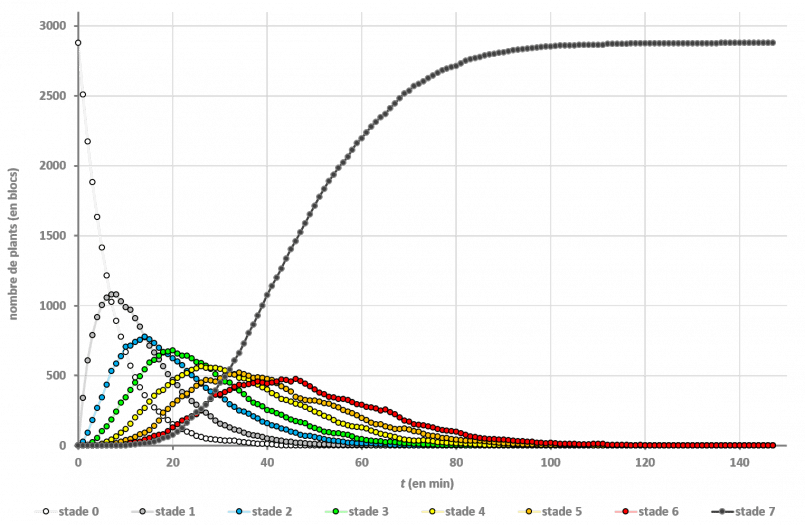
Les études “en plein champ” ont donné les résultats suivants :
On n’a même pas besoin de passer par les mathématiques pour voir que c’est la culture en bandes qui est la plus efficace : si on regarde le dernier stade de croissance, on voit que la moitié du champ en bandes est à maturité au bout de 24 minutes, alors que les autres dispositions le sont bien plus tard (à 46 minutes).
Cela va dans le sens de toutes les vidéos produites jusque-là : la configuration en bandes permet d’aller 2 fois plus rapidement. Mais on n’a pas l’explication du pourquoi.
![]()
Théorie de la croissance des plantes
Si on veut répondre au pourquoi, il va falloir expliciter le mécanisme par lequel pousse les plantes. Nous allons donc théoriser et transposer en équations pour obtenir un modèle mathématique. Si le modèle donne des prédictions proches de l’expérimentation, on pourra considérer que la description est correcte.
 La croissance d’une plante peut être vue comme une succession d’étapes successives, où une plante passe d’un stade à un autre dans un ordre précis.
La croissance d’une plante peut être vue comme une succession d’étapes successives, où une plante passe d’un stade à un autre dans un ordre précis.
Par la suite, on définira un ensemble de fonctions $ \left ( B_n \right ) $, qui sont l’ensemble des plantes du champ au stade $n$. $n$ est un entier allant de 0 (premier stade) à 7 (plante à maturité).
Concrètement, cet ensemble de fonctions à pour variable le temps : $$B_n : t \mapsto B_n(t)$$ A tout instant $t$ de l’expérience, la fonction $B_n$ donne le nombre de plantes au stade $n$ présent dans mon champ, sous la forme d’un nombre noté $B_n(t)$.
Si je ne sème ni ne détruit de plants durant l’expérience, la somme de ces fonctions est une constante à tout instant $t$ : $$ B_0(t) + B_1(t) + \cdots + B_7(t) = \sum_{n=0}^7 B_n(t) = N$$
Avec $N$ le nombre total de plantes présentes dans le champ.
 Chaque flèche représente une étape de transformation et reflète le fonctionnement du jeu.
Chaque flèche représente une étape de transformation et reflète le fonctionnement du jeu.
Imaginons le champ à un instant $t$. Après un délai $\delta t$ très petit, le jeu a eu le temps de faire qu’une seule étape :
- le jeu choisit au hasard une plante dans le champ, comme il tirerait une boule dans une urne.
- avec de nombreux facteurs externes (les voisins, l’éclairage, l’humidification du sol, que sais-je), le jeu va décider si cette plante va grandir ou pas.
Si on s’intéresse maintenant à une vision globale et des intervalles de temps plus importants, on peut dire modéliser la vitesse de transformation $\left \{ n \right \} \rightarrow \left \{ n+1\right \}$, notée $v_n$, ainsi : $$v_n(t) = k_n \, B_n(t)$$
- La probabilité que la plante choisie soit au stade $n$ est directement proportionnelle au nombre de plantes à l’état $n$ à l’instant $t$, autrement dit à $B_n(t)$. Plus un stade est représenté, plus il a de chances d’être sélectionné.
- L’ensemble des facteurs externes modulant la transformation peut être représentée par une constante $k_n \geq 0$ : plus cette constante est importante, plus la transformation est rapide.
Comme on ne sait pas si le stade de la plante influence la vitesse de transformation, on pose donc 7 constantes $(k_n)$, une pour chaque transformation.
 Mais si on considère le nombre de plantes à un stade $n$, il faut considérer deux effets :
Mais si on considère le nombre de plantes à un stade $n$, il faut considérer deux effets :
- la transformation $\left \{ n -1 \right \} \rightarrow \left \{ n\right \}$ va augmenter $B_n$.
- la transformation $\left \{ n \right \} \rightarrow \left \{ n + 1\right \}$ va diminuer $B_n$.
En utilisant la dérivée $\dfrac{\text{d} \, B_n}{\text{d} t}$ pour représenter comment varie $B_n$ au cours du temps, on peut donc écrire que : $$\frac{\text{d} \, B_n}{\text{d} t} = v_{n-1} – v_n$$ Et finalement, en remplaçant avec ce qu’on a vu précédemment : $$\frac{\text{d} \, B_n (t)}{\text{d} t} = k_{n-1} \; B_{n-1}(t) – k_n \; B_n(t) $$
 Au final, nous avons donc un système de 8 équations pour décrire les 8 fonctions $(B_n)$ :
Au final, nous avons donc un système de 8 équations pour décrire les 8 fonctions $(B_n)$ :
- pour le premier stade $n=0$, l’équation reflète une diminution :
- $$\frac{\text{d} \, B_0 (t)}{\text{d} t} = – k_0 \; B_0(t) $$
- pour les 6 stades intermédiaires $1 \leq n \leq 6$, les variations dépendent de deux mécanismes :
- $$\frac{\text{d} \, B_n (t)}{\text{d} t} = k_{n-1} \; B_{n-1}(t) – k_n \; B_n(t) , \; n \in [\![ 1 ; 6 ]\!] $$
- pour le dernier stade $n=7$, c’est une augmentation :
- $$\frac{\text{d} \, B_7 (t)}{\text{d} t} = k_6 \; B_6(t)$$
On a posé mathématiquement un système d’équations différentielles, les dérivées des fonctions dépendant de combinaisons linéaires des fonctions. Reste à résoudre ce système.
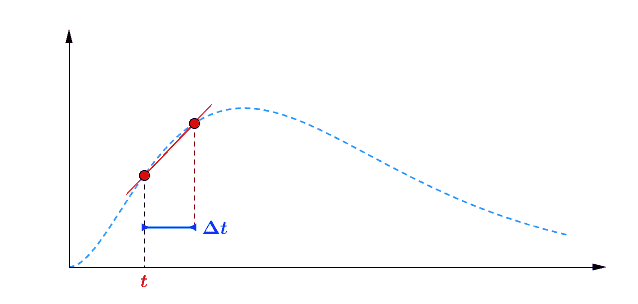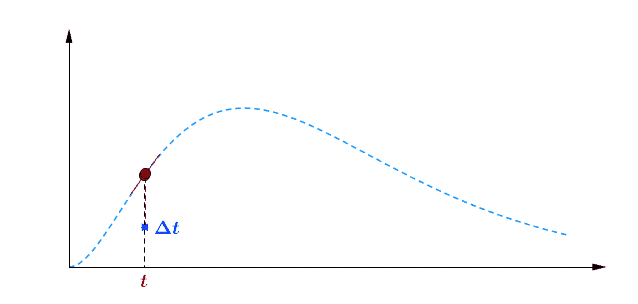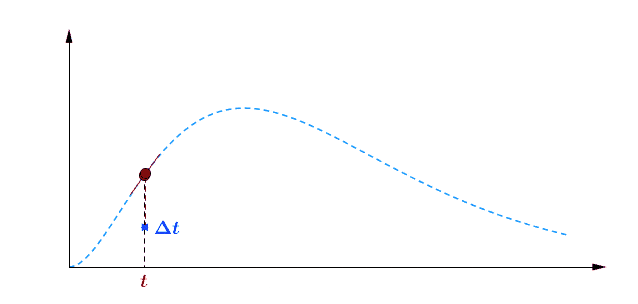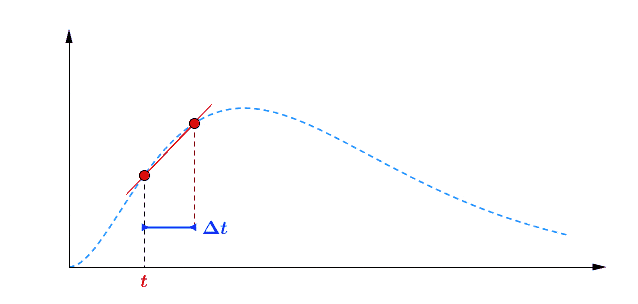
Pour avoir une idée de comment varie au cours du temps, je peux par exemple faire deux mesures à des instants différents et comparer : $$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} \begin{matrix} Ici, on observe une augmentation. Durant une durée $\Delta t = t_2 – t_1 = $ 5 min, le nombre de plantes au stade 2 a augmenté de $\Delta B_2 = B_2(t_2) – B_2(t_1) = $294 plantes. Pour se représenter cette augmentation, on peut aussi raisonner avec la quantité suivante : $$\frac{\Delta B_2}{\Delta t} = \frac{B_2(t_2)-B_2(t_1)}{t_2-t_1} = 58.8 \; \text{plantes/min}$$ Graphiquement, cette quantité correspond à la pente de la droite entre les deux points de mesure sur la courbe. Le grand avantage de cette quantité est de quantifier numériquement les variations de : On peut donc dire qu’en moyenne, durant cette période de 5 minutes, $B_2$ a augmenté de 59 plantes chaque minute. Mais est-ce que ce nombre représente fidèlement ce qu’il s’est passé ? En consultant la courbe, vous pouvez vous convaincre que non : on a eu certes une augmentation, mais la seconde mesure a eu lieu pendant que $B_2$ commençait à diminuer… Dans un monde idéal, pour suivre exactement comment la fonction varie au moment de la première mesure, il faudrait faire la seconde mesure à un instant très proche, voire même infiniment proche (faire tendre le délai $\Delta t$ vers une durée proche de 0). C’est ça, la dérivée à un instant $t$ : calculer la variation locale de notre fonction en considérant deux mesures séparées d’un délai extrêmement petit. En utilisant une notation plus qu’abusive, on écrira la dérivée de $B_2$ comme ceci : $$\frac{\text{d} B_2(t)}{\text{d}t} = \lim_{\Delta t \rightarrow 0} \frac{B_2(t+\Delta t) – B_2(t)}{\Delta t}$$ Si vous devez retenir une chose de la dérivée, c’est une fonction qui permet de quantifier comment varie la fonction associée. Il est bien beau d’écrire des équations, mais c’est encore mieux si on peut les résoudre. Commençons par le début, le tout premier stade $n=0$ : Si vous avez déjà un certain passif en mathématiques ou en physique, vous devez reconnaître cette allure de courbe qui fait penser à une décroissance exponentielle : $B_0$ décroit rapidement au départ, puis la transformation ralentie de plus en plus pour ne plus évoluer une fois le zéro atteint. $\dfrac{\text{d} \, B_0 (t)}{\text{d} t} = – k_0 \; B_0(t) $ Il s’agit d’une équation différentielle du premier ordre, et sa résolution est au programme des terminales scientifiques. La forme générale des solutions est : $t \mapsto C^{ste} \cdot \exp (-k_0 \, t)$ Avec $C^{ste}$ qui dépend des conditions initiales. Au début de l’expérience, $t=0$ et le champ contient $N$ plantes au stade 0, donc : $B_0(0) = N = C^{ste} \cdot \exp{0} = C^{ste}$ Pour finalement écrire notre équation d’évolution : $B_0(t) = N \cdot \exp (-k_0 \, t)$ Pour ceux qui veulent plus de détails, les grandes lignes sont expliquées dans l’onglet ci-dessous. En utilisant la fonction logarithme népérien (réciproque de l’exponentielle), on obtient une fonction linéaire : $B_0(t) = N \cdot \exp (-k_0 \, t) \Leftrightarrow – \ln \left ( \dfrac{B_0(t)}{N} \right ) = k_0 \cdot t$ L’avantage d’une fonction linaire, c’est qu’elle permet de juger d’un simple coup d’œil si le modèle correspond ou non. En effet, il est plus facile pour un humain (et un ordinateur pour calculer un coefficient de régression $R^2$) de raisonner sur des droites et des points qui sont censés être alignés. Ici, la correspondance est plutôt satisfaisante. Comme l’incertitude augmente au fur et à mesure du temps $t$, il n’est pas étonnant que les derniers points soient plus à l’écart. Et le coefficient de régression linéaire $R^2$ est proche de 1, ce qui valide le modèle. Pour ceux qui veulent plus de détails sur ces fonctions, elles sont développées dans l’onglet ci-dessous. Remarquez qu’il est plus difficile de voir sous cette forme que les différences notamment vers le plateau de la fin de la courbe. Mais avant de résoudre notre équation, il faut s’intéresser à quelque chose de simple, par exemple : est-ce qu’il existe des fonctions qui est sont égale à leur propre dérivée ? $$ \frac{\text{d} f}{\text{d} t} = f$$ Non seulement on peut démontrer que des solutions existent, mais on peut même démontrer qu’on a une solution unique si on pose une condition. Par exemple, si je pose :$$f(0)=1$$ On a une unique solution, qu’on nomme la fonction exponentielle exp :$$\left.\begin{matrix} Pour obtenir toutes les autres fonctions, il suffit de la multiplier par une constante puisque nous avons : $$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} \begin{matrix} Je précise que ceci est n’est pas une réelle démonstration, mais simplement l’essence du raisonnement de la démonstration. Maintenant, si on a une constante multiplicative dans l’exponentielle, la fonction de départ se voit multiplier par la constante après dérivation : La fonction logarithme népérien, notée ln, est ce qu’on appelle en mathématiques la fonction réciproque de l’exponentielle. Imaginons que vous êtes un prestidigitateur faisant un tour de nombre : vous demandez à votre volontaire de choisir un nombre, puis vous lui faites faire quelques opérations et lui demandez le résultat. Pour que le tour soit spectaculaire, le résultat n’a souvent rien d’évident pour distinguer le nombre de départ. Mais vous devez avoir un moyen d’annuler rapidement toutes ces opérations : c’est ça qu’on appelle la fonction réciproque. $$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} x \; \xrightarrow[{\color{Blue} \text{spectateur}}]{\exp} \; \exp(x) \; \xrightarrow[{\color{Blue} \text{magicien}}]{\ln} \; x$$ Voilà les grandes lignes. Pour aller plus loin, un bon livre de mathématiques sera nécessaire. Nous avons donc résolu plutôt facilement le cas $n=0$, mais les choses vont se corser et nous allons même créer un nouveau circuit pour le reste de l’étude : /fill -30 21 -30 -32 21 -32 minecraft:wheat $n$ replace minecraft:wheat /execute @e[team=Sensor] ~ ~ ~ /clone -32 21 -32 -30 21 -30 ~-1 21 ~-1 Toutes les zones sont hydratées, isolées les unes des autres par au moins une bordure d’un bloc de large et l’éclairage est constant. Une première remarque vient sur le fait qu’on peut accélérer la croissance des plantes en changeant le randomTickSpeed, mais il faut diminuer la période de l’horloge en respectant : $\left [ \, \text{randomTickSpeed} \, \right ] \times \left [ \, \text{Periode} \, \right ] = 3 \times 1 \,200 = 3 \, 600$ Si vous multipliez par 30 le randomTickSpeed, il faudra diviser par 30 la période de l’horloge. Deux effets apparaissent et se compensent en partie : En testant différentes combinaisons, la reproductibilité est satisfaisante (avec une erreur de l’ordre de 0.1%) avec un randomTickSpeed de 60. C’est ce qui servira pour les données suivantes. Une seconde remarque vient sur les données qui sont collectées : Revenons à l’équation qui définit le nombre de plantes au stade $n$ : $\dfrac{\text{d} \, B_n (t)}{\text{d} t} = k_{n-1} \; B_{n-1}(t) – k_n \; B_n(t)$ L’idéal serait d’avoir une équation aussi simple que celle que nous avons déjà résolu au stade 0. C’est possible, mais il faut s’arranger pour ne jamais avoir de plantes au stade $n-1$ : $\forall t \in \mathbb{R}^+, \, B_{n-1}(t) = 0 \; \Rightarrow \; \dfrac{\text{d} \, B_n (t)}{\text{d} t} = – k_n \; B_n(t)$ Il suffit donc de débuter l’expérience avec tous les plants de blé au stade $n$, et on pourra tracer la régression linéaire comme précédemment. Ce sont les 7 courbes qui suivent. Compte-tenu des écarts statistiques, on peut considérer que les constantes de vitesse sont identiques, ce qui permettent de simplifier énormément les calculs. Ainsi, pour les plantes au stade 1, si $k_0 \neq k_1$ : $$B_1 (t) = N \, k_1 \frac{\exp(-k_0 \, t) – \exp(- k_1 \, t)}{k_1 – k_0}$$ Le fait que les constantes soient égales nous arrange beaucoup, car le cas $k_1=k_0$ est beaucoup plus digeste : $$B_1 (t) = N \, k_0 \, t \exp(-k_0 \, t)$$ Nous avons donc des expressions analytiques simples qui donnent des résultats satisfaisants, super! Pour le détail de la résolution mathématique, ouvrez l’onglet. Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_0 \, : \, t \mapsto N \, \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \, \text{min} ^{-1}$ $R^2=0.9952$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_1 \, : \, t \mapsto N \, k_0 \, t \, \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9918$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_2 \, : \, t \mapsto \dfrac{N}{2} \, k^2_0 \, t^2 \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9915$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_3 \, : \, t \mapsto \dfrac{N}{6} \, k^3_0 \, t^3 \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9951$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_4 \, : \, t \mapsto \dfrac{N}{24} \, k^4_0 \, t^4 \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9924$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_5 \, : \, t \mapsto \dfrac{N}{120} \, k^5_0 \, t^5 \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9956$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_6 \, : \, t \mapsto \dfrac{N}{720} \, k^6_0 \, t^6 \exp (- k_0 \, t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9876$ Statistiques faites sur $N=20 \, 000$ plants isolés initialement au stade 0, modèle tracé en noir. Équation du modèle : $B_7 \, : \, t \mapsto N- B_0(t) – B_1(t) – B_2(t) – B_3(t) – B_4(t) – B_5(t) – B_6(t)$ avec $k_0 = 0.2935 \, \text{plantes} \cdot \text{min} ^{-1}$ $R^2=0.9995$ On a déjà résolu la première équation différentielle : $B_0 (t) = N \; \exp ( – k_0 \; t )$. Détaillons le calcul pour $B_1(t)$ : $\dfrac{\text{d} B_1(t)}{\text{d}t} = k_0 \; B_{0}(t) – k_0 \cdot B_1(t)$ Qu’on peut ré-écrire de la façon suivante en remplaçant $B_0(t)$ par son expression : $$\frac{\text{d} \, B_1(t)}{\text{d}t} + k_0 \; B_1(t) = k_0 \, N \exp(-k_0 \, t)$$ Posons $B_1(t) = Q(t) \cdot \exp{-k_0 \cdot t}$, avec $Q(t)$ une fonction à déterminer. Rappelons la forme de la dérivée d’un produit de fonctions dérivables : Donc dériver $B_1(t) = Q(t) \cdot \exp(-k_0 \cdot t)$ donne : $\dfrac{\text{d} \, B_1(t)}{\text{d}t} = – k_0 \; \exp(-k_0 \; t) \; Q(t) + \exp(-k_0 \; t) \; \dfrac{\text{d} \, Q(t)}{\text{d}t}$ Et l’équation différentielle se retrouve simplifiée des exponentielles : Qui s’intègre avec les conditions initiales : $Q(t) = k_0 \; N \; t$ et finalement : $$B_1(t) = N \; k_0 \, t \, \exp(- k_0 \, t) = k_0 \, t \, B_0(t)$$ Passons maintenant à $B_2(t)$, l’équation est très similaire : $\dfrac{\text{d} B_2(t)}{\text{d}t} + k_0 \cdot B_2(t) = k_0 \; B_1(t) = N \; k^2_0 \, t \, \exp(- k_0 \, t) $ Et en posant, de même, $B_2(t) = Q(t) \cdot \exp{-k_0 \cdot t}$, on obtient $\dfrac{\text{d} \, Q(t)}{\text{d}t}= N k^2_0 \, t$ En regardant comment s’intègre les fonctions puissance : $$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} \begin{matrix} Finalement $B_2(t) = \dfrac{N}{2} \, k_0^2 \, t^2 \exp(-k_0 \, t) = \dfrac{(k_0 \, t )^2}{2} \, B_0(t)$ Recommençons avec $B_3(t)$ : vous commencez à connaitre la forme de l’équation différentielle. $\dfrac{\text{d} B_3(t)}{\text{d}t} + k_0 \cdot B_3(t) = k_0 \; B_2(t) = \dfrac{N}{2} \, k_0^3 \, t^2 \exp(-k_0 \, t)$ Qu’on résout, en posant $B_3(t) = Q(t) \, \exp(-k_0 \, t)$, ce qui simplifie la résolution : $\dfrac{\text{d} \, Q(t)}{\text{d}t}= \dfrac{N}{2} k^3_0 \, t^2 \Rightarrow Q(t)=\dfrac{N}{6} k^3_0 \, t^3$ Et finalement, la résolution donne $B_3(t) = \dfrac{N}{6} k^3_0 \, t^3 \exp(-k_0 \, t) = \dfrac{(k_0 \, t)^3}{3 \, !} B_0(t)$, avec $n \, !$ la factorielle définie par $$n \, ! = \prod_{j=1}^n j = 1 \times 2 \times \cdots \times (n-1) \times n$$ Vous pouvez donc commencer à voir une récurrence : en effet, lorsqu’on passe de $B_n(t)$ à $B_{n+1}(t)$, on a l’ajout de : On dégage une forme générale, que vous pouvez vous amuser à démontrer par récurrence : $B_n(t)=\dfrac{(k_0 \, t)^n}{n \, !} B_0(t) = \dfrac{(k_0 \, t)^n}{n \, !} N \exp(- k_0 \, t)$ avec $n \in \left \{ 0 \, ; \, \cdots \, ; \, 6 \right \}$ Et pour résoudre la dernière équation différentielle, on utilise le fait que le nombre de plantes total est constant : $$B_0(t) + B_1(t) + \cdots + B_7(t) = \sum_{n=0}^7 B_n(t) = N$$ Ainsi, $$B_7(t) = N – \sum_{n=0}^6 B_n(t) = N \left [ 1 – \sum_{n=0}^6 \dfrac{(k_0 \, t)^n}{n \, !} \exp(- k_0 \, t) \right ]$$ Félicitations, nous avons nos expressions pour tous les stades ! Maintenant qu’on sait comment la croissance s’effectue, on va pouvoir (enfin) s’attaquer au sujet de l’étude : l’action du voisinage sur la croissance. Initialement, le blé est au stade 0. A partir de 10 000 plantes, on construit la régression linéaire de la première étape de la croissance. La pente de la régression obtenue ici est : $$k_0=0.2988 \, \text{plantes} \, \text{min} ^{-1}$$ La régression linéaire apparaîtra en rouge pour servir de point de comparaison. Nous avons donc une première règle sur la croissance des plantes : si un bloc est placé en diagonale, la nouvelle constante est $\dfrac{k_0}{2}$. Deuxième règle donc : si 2 blés voisins forment un angle droit, la nouvelle constante devient $\dfrac{k_0}{2}$. Vous remarquez également qu’il ne s’agit pas d’un effet cumulatif : $k’_0$ diminue si une des règles est vérifié, mais elle reste à une valeur de $\dfrac{k_0}{2}$. Cela fonctionne en remplaçant les carottes par des pommes de terre et le rôle est symétrique : le blé n’influence pas la pousse des carottes et inversement. Conclusion : faire des cultures en bandes permets de mieux rentabiliser votre temps, doublant la production horaire par rapport au champ classique. Nous avons terminé nos expérimentations sur la disposition des cultures. Nous avons étudié et illustré comment la croissance des plantes étaient gérées par le jeu, en montrant notamment que les plantes voisines pouvait diminuer la vitesse de pousse. Nous avons confirmé que la disposition en bandes permettaient le meilleur rendement horaire. J’espère que cet article vous aura intéressé et que vous avez eu autant de plaisir à le lire que moi à l’écrire. N’hésitez pas à donner vos retours dans les commentaires, ainsi que des expériences que vous voudriez tester sur les mécaniques de jeu dans Minecraft (je remercie d’ailleurs The_MurmeX pour son commentaire avec ce sujet). À bientôt dans la TestZone. Pour tester par vous-même, voici le monde de test utilisé pour obtenir les résultats présentés :Un peu de théorie : la dérivée

{\color{Blue} t} & {\color{Blue} B_2(t)} \\
t_1 = 3 \text{ min} & B_2(t_1)= 457 \text{ plantes}\\
t_2 = 3 \text{ min} & B_2(t_2)= 751 \text{ plantes}
\end{matrix}$$
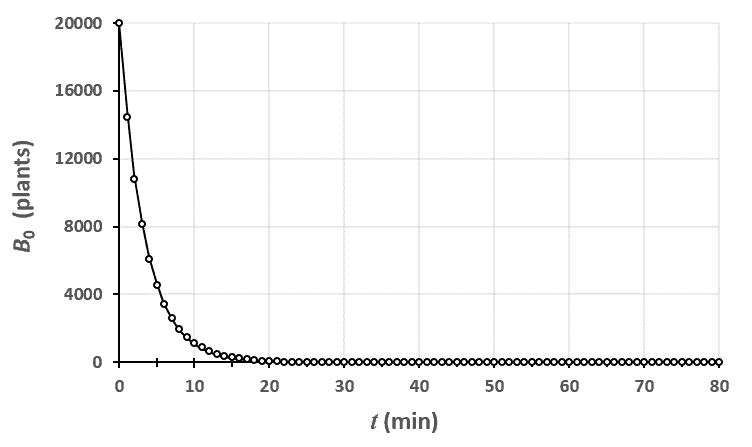
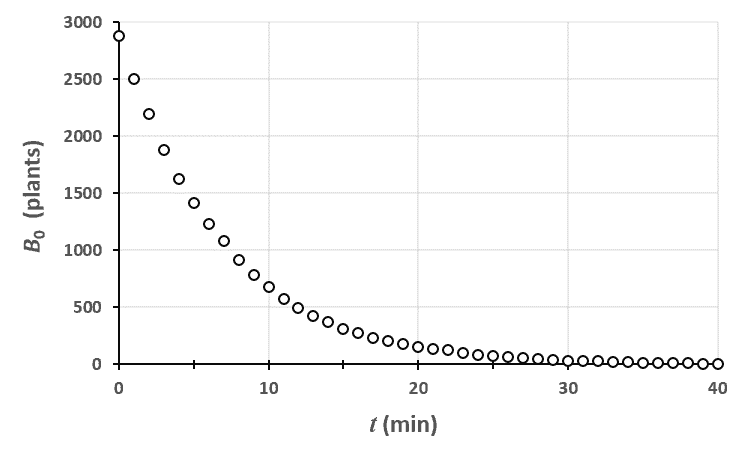 Ci-dessus, on a représenté le nombre de plantes au stade $n=0$ en fonction du temps. Le champ était un rectangle entièrement rempli de 2880 plants de blé, tous au stade 0 à $t=0$.
Ci-dessus, on a représenté le nombre de plantes au stade $n=0$ en fonction du temps. Le champ était un rectangle entièrement rempli de 2880 plants de blé, tous au stade 0 à $t=0$.
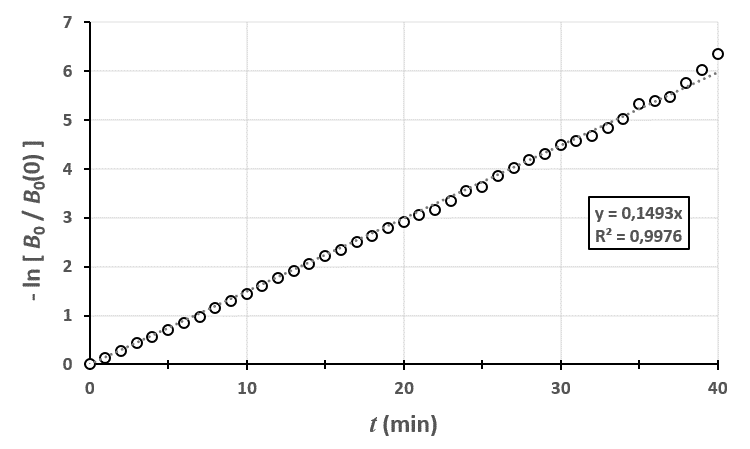
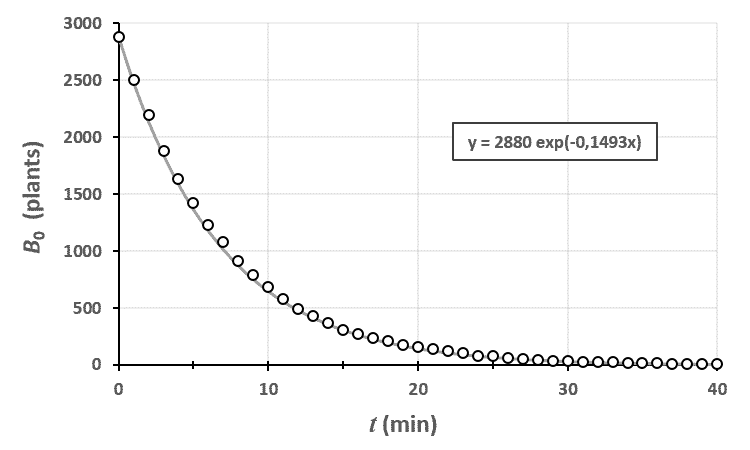 En traçant le modèle théorique avec les données brutes, on peut voir que le modèle est assez proche de la réalité. En fait, plus votre champ est grand, plus vous réduisez l’importance des fluctuations dues au hasard et plus vous serez proches de cette courbe.
En traçant le modèle théorique avec les données brutes, on peut voir que le modèle est assez proche de la réalité. En fait, plus votre champ est grand, plus vous réduisez l’importance des fluctuations dues au hasard et plus vous serez proches de cette courbe.
Un peu de théorie : équations différentielles, exponentielle et logarithme népérien
\dfrac{\text{d} f}{\text{d} t} = f \\
f(0)=1
\end{matrix}\right\} \Rightarrow f : t \mapsto \exp(t)$$
\dfrac{N \cdot \exp(x) – N \cdot \exp(t)}{x-t} & = & N \times \dfrac{\exp(x) – \exp(t)}{x-t}\\ \\
\downarrow \; \; \underset{x \to t}{\lim} & \, & \downarrow \; \; \underset{x \to t}{\lim}\\ \\
{\color{Red} \dfrac{\text{d}}{\text{d}t} \left [ N \cdot \exp(t) \right ]} & {\color{Red} =} & {\color{Red} N \cdot \exp(t)}
\end{matrix}$$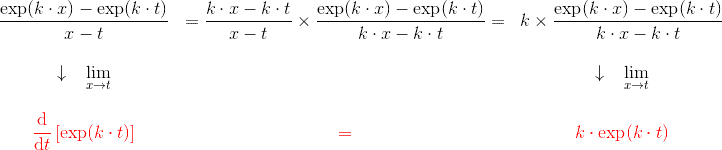 D’où l’omniprésence de cette exponentielle dans les équations qui vont suivre.
D’où l’omniprésence de cette exponentielle dans les équations qui vont suivre.
 Le précédent montage reproduisait des conditions d’agriculture classique, mais il n’est pas très souple pour tester différents paramètres :
Le précédent montage reproduisait des conditions d’agriculture classique, mais il n’est pas très souple pour tester différents paramètres :
 Le principe global est le suivant :
Le principe global est le suivant :
 Nous avons posé au départ que les transformations pouvaient avoir des vitesses différentes en fonction de stade concerné. On a donc défini 7 constantes $k_n$ dans nos équations, chacune reflétant l’influence des paramètres extérieurs sur la transformation $\left \{ n \right \} \rightarrow \left \{ n+1 \right \}$. Reste à déterminer ces constantes.
Nous avons posé au départ que les transformations pouvaient avoir des vitesses différentes en fonction de stade concerné. On a donc défini 7 constantes $k_n$ dans nos équations, chacune reflétant l’influence des paramètres extérieurs sur la transformation $\left \{ n \right \} \rightarrow \left \{ n+1 \right \}$. Reste à déterminer ces constantes.
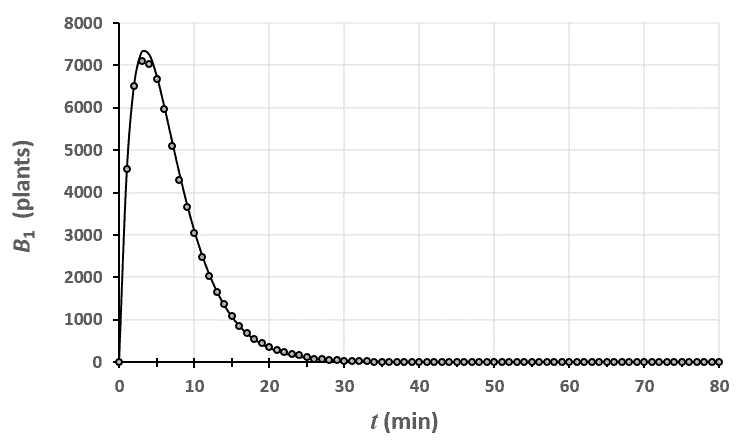
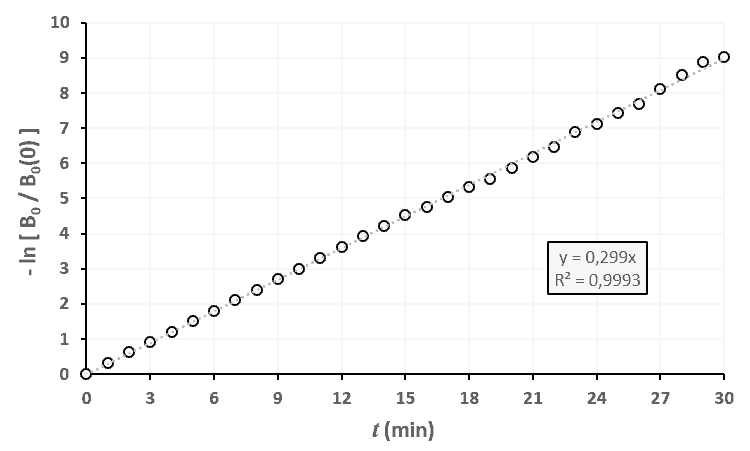 Statistiques faites sur 50 000 plants de blé isolés au stade 0.
Statistiques faites sur 50 000 plants de blé isolés au stade 0.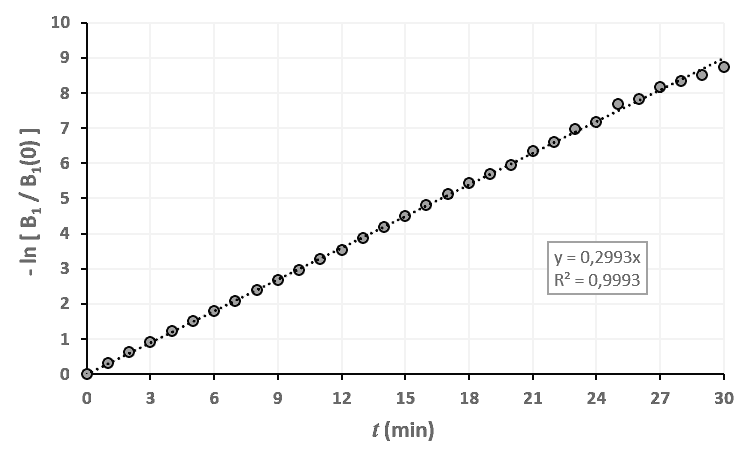 Statistiques faites sur 50 000 plants de blé isolés au stade 1.
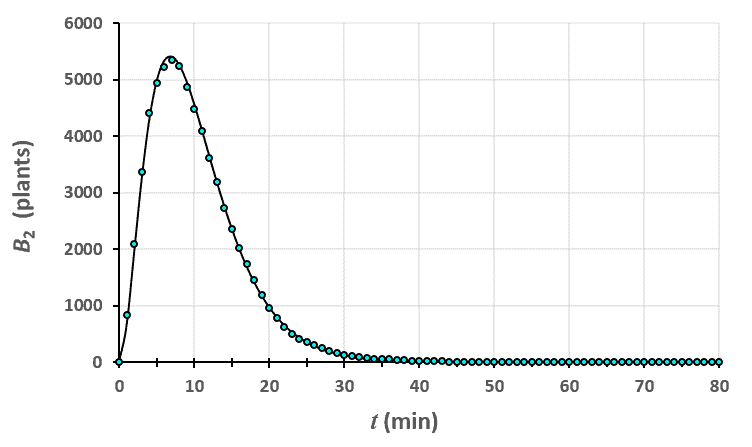
Statistiques faites sur 50 000 plants de blé isolés au stade 1.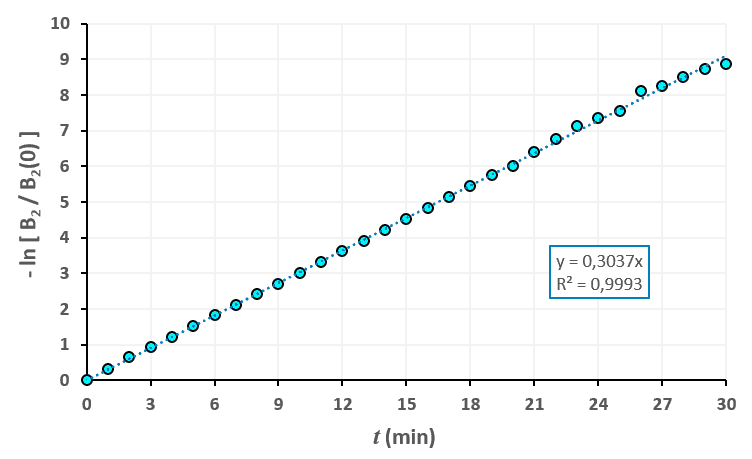 Statistiques faites sur 50 000 plants de blé isolés au stade 2.
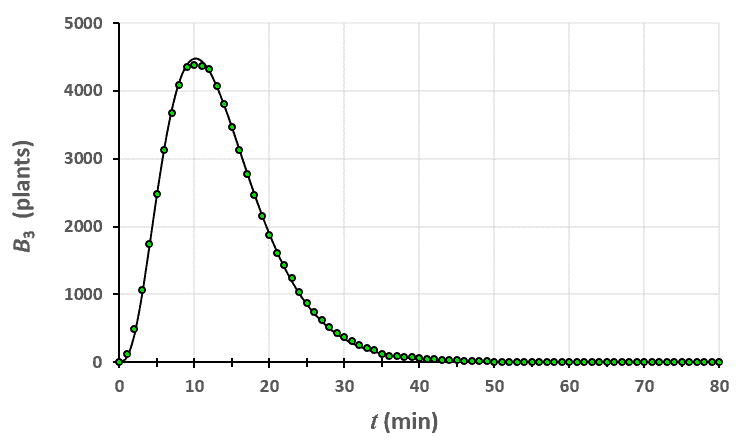
Statistiques faites sur 50 000 plants de blé isolés au stade 2.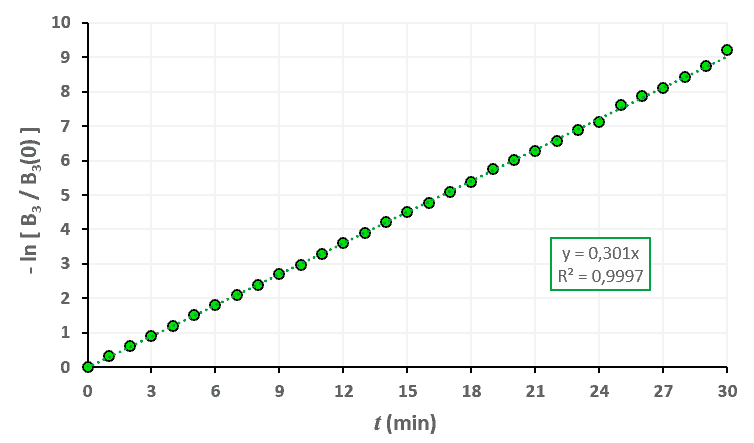 Statistiques faites sur 50 000 plants de blé isolés au stade 3.
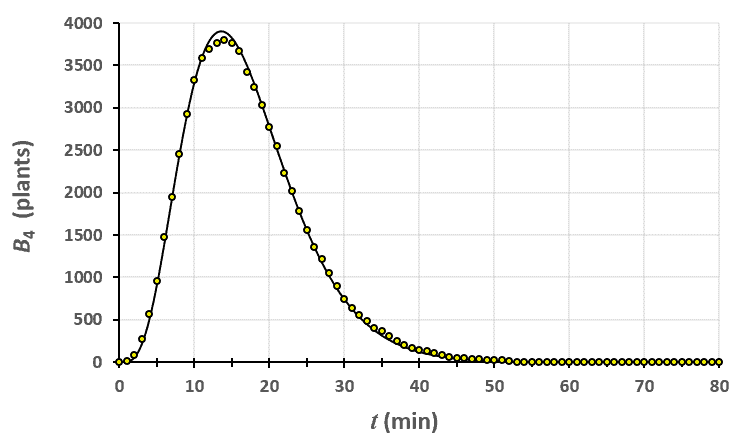
Statistiques faites sur 50 000 plants de blé isolés au stade 3.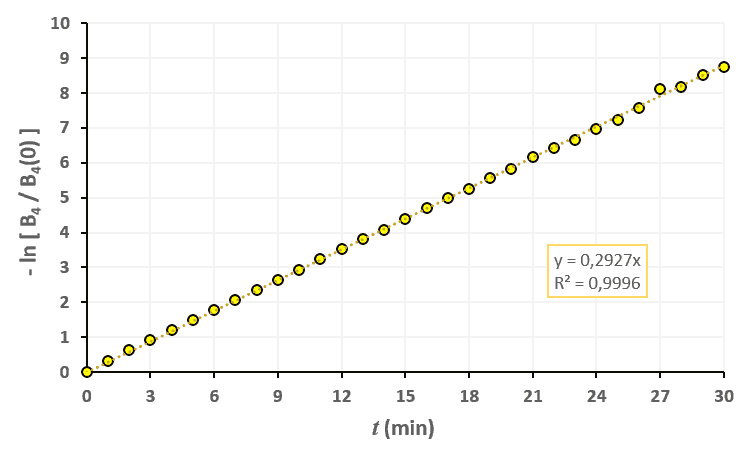 Statistiques faites sur 50 000 plants de blé isolés au stade 4.
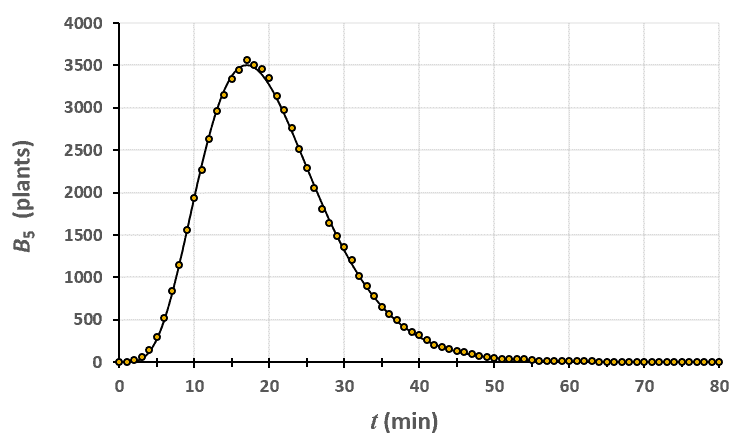
Statistiques faites sur 50 000 plants de blé isolés au stade 4.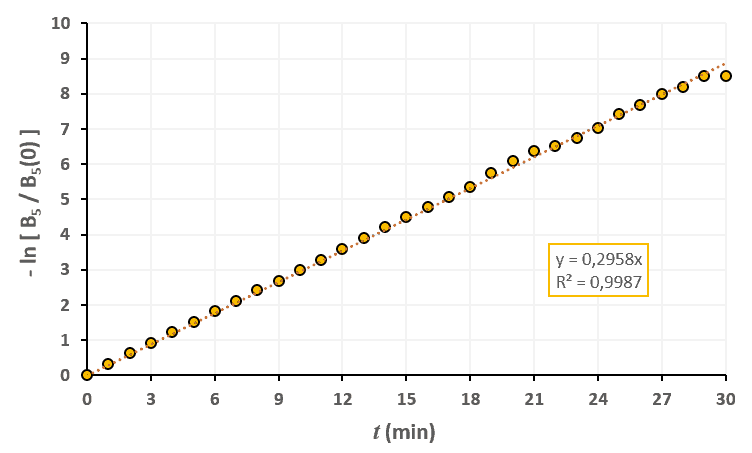 Statistiques faites sur 50 000 plants de blé isolés au stade 5.
Statistiques faites sur 50 000 plants de blé isolés au stade 5.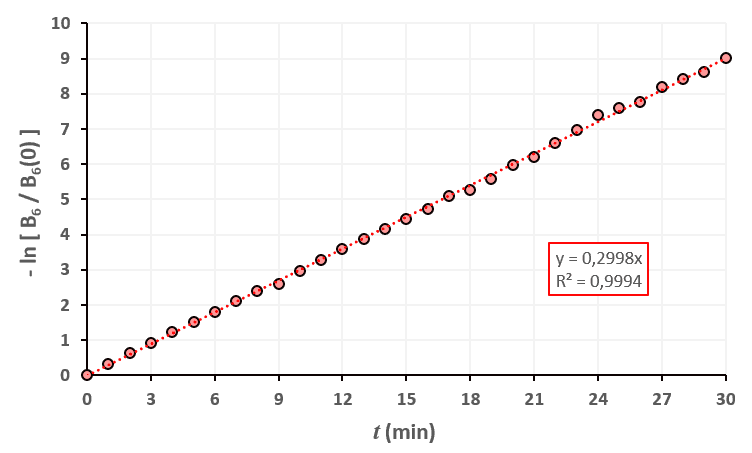 Statistiques faites sur 50 000 plants de blé isolés au stade 6.
Statistiques faites sur 50 000 plants de blé isolés au stade 6.
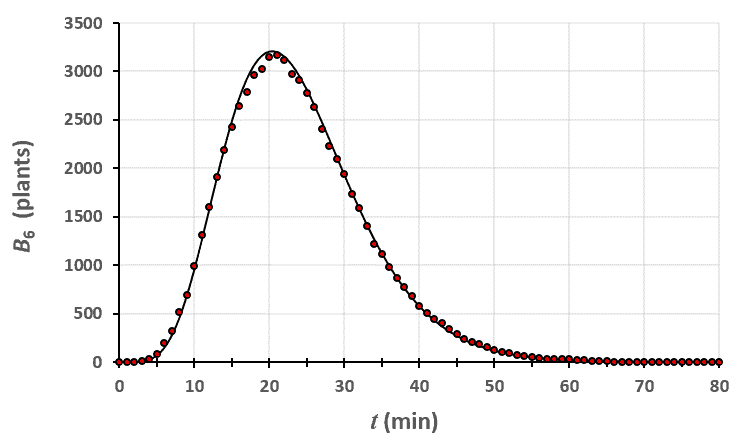
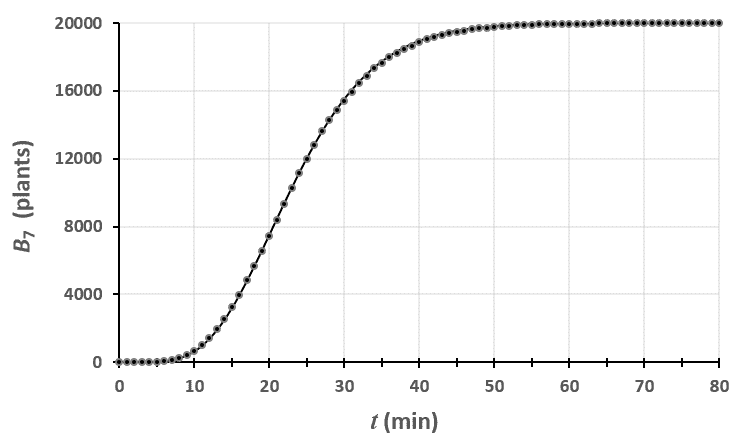
Un peu de théorie : résolution exacte du système
\dfrac{\text{d} B_0(t)}{\text{d}t} = – k_0 \; B_0(t) &\\
\dfrac{\text{d} B_n(t)}{\text{d}t} = k_{n-1} \; B_{n-1}(t) – k_n \; B_n(t) & \text{avec } n \in \left \{ 1 \, ; \, \cdots \, ; \, 6 \right \}\\
\dfrac{\text{d} B_7(t)}{\text{d}t} = k_6 \; B_6(t) &
\end{matrix}\right.$$ Ici, on va résoudre le système en considérant que $ k_0 = k_1 = \cdots = k_6$ : $$\left\{\begin{matrix}
\dfrac{\text{d} B_0(t)}{\text{d}t} = – k_0 \; B_0(t) &\\
\dfrac{\text{d} B_n(t)}{\text{d}t} = k_0 \; \left [B_{n-1}(t) – B_n(t) \right ] & \text{avec } n \in \left \{ 1 \, ; \, \cdots \, ; \, 6 \right \}\\
\dfrac{\text{d} B_7(t)}{\text{d}t} = k_0 \; B_6(t) &
\end{matrix}\right.$$
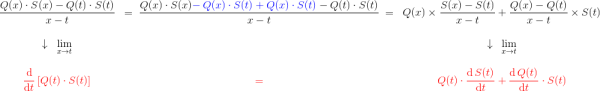
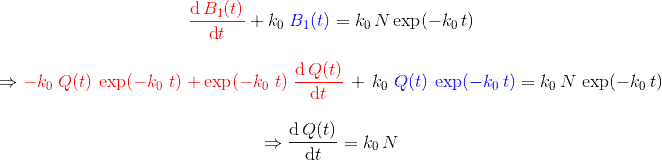
\dfrac{x^n – t^n}{x-t} & = & \underset{n \text{ termes}}{\underbrace{x^{n-1} + x^{n-2} \; t + \cdots + x \; t^{n-2} + t^{n-1}}} \\ \\
\downarrow \; \; \underset{x \to t}{\lim} & \, & \downarrow \; \; \underset{x \to t}{\lim}\\ \\
{\color{Red} \dfrac{\text{d}}{\text{d}t} \left [ \, t^n \, \right ]} & {\color{Red} =} & {\color{Red} n \, t^{n-1}}
\end{matrix}$$ On déduit que $\dfrac{\text{d}}{\text{d}t} \left [ \, \dfrac{t^{n+1}}{n+1} \, \right ] = t^n$, donc $Q(t) = \dfrac{N}{2} \, k_0^2 \, t^2$.
![]()
Action du voisinage sur la vitesse de pousse
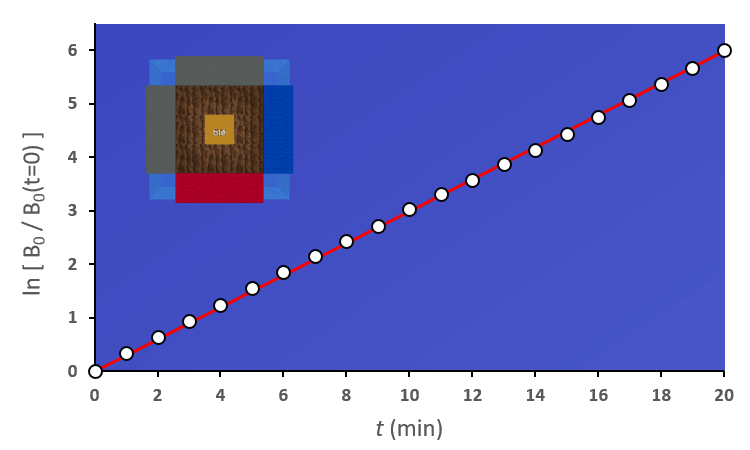 Pour pouvoir faire des comparaisons, il nous faut une référence :
Pour pouvoir faire des comparaisons, il nous faut une référence :
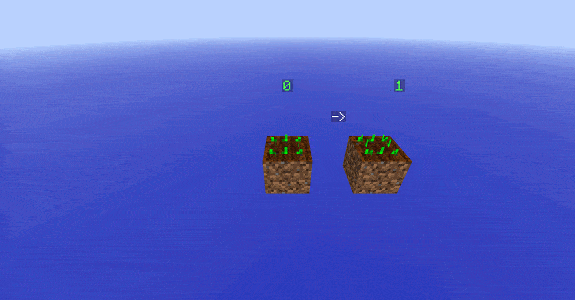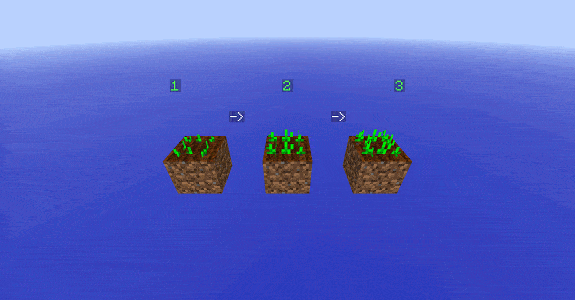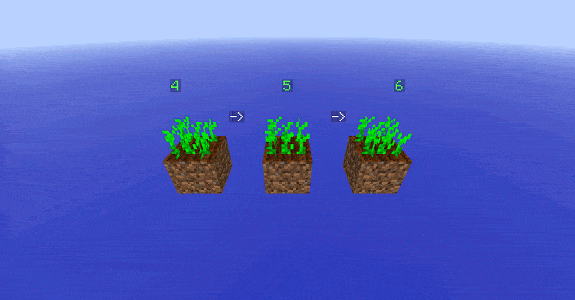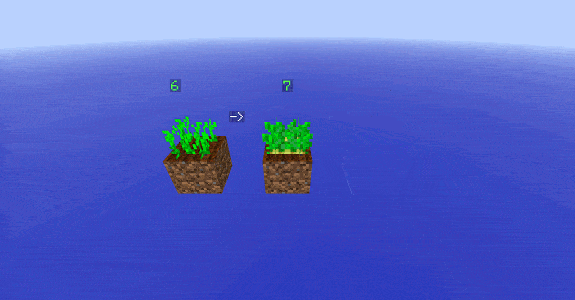
 Plaçons un premier blé voisin : il y a au total 8 possibilités de le placer autour du blé central. On distingue deux cas :
Plaçons un premier blé voisin : il y a au total 8 possibilités de le placer autour du blé central. On distingue deux cas :
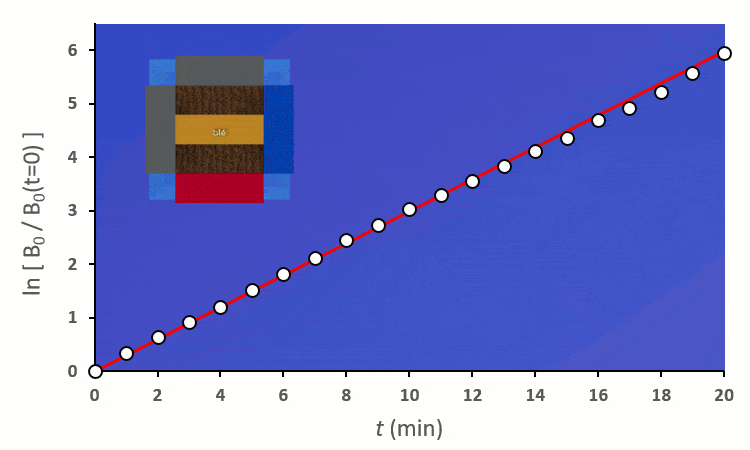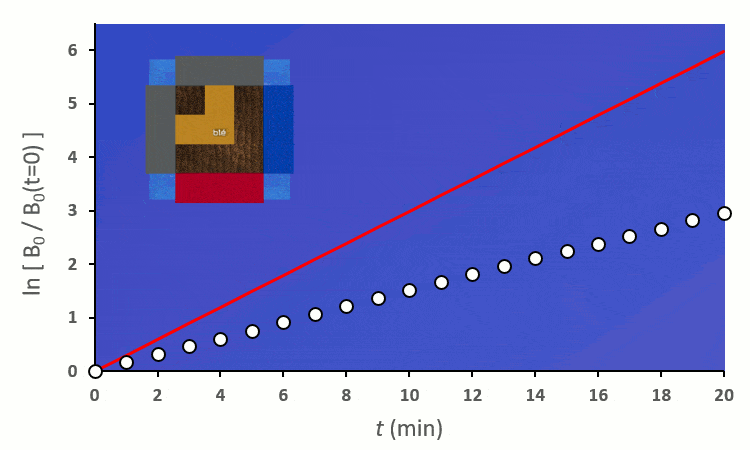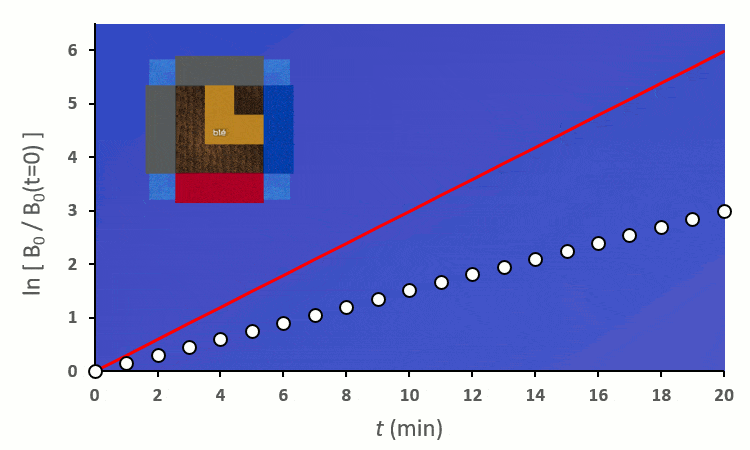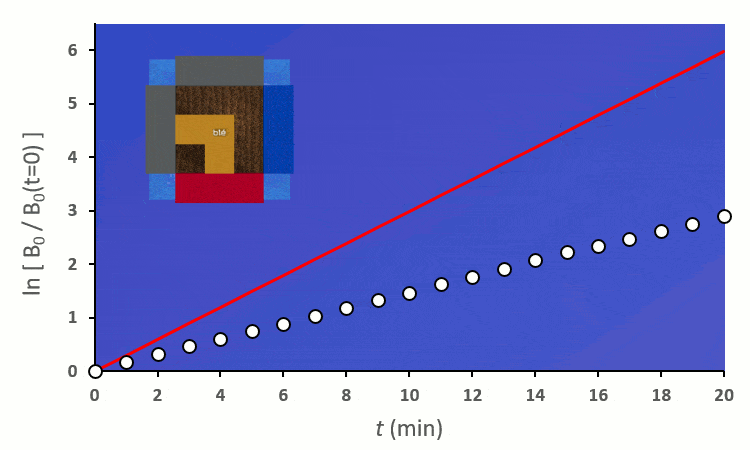 En excluant toutes les situations où un blé voisin se trouve en diagonale (nous verrons plus tard pourquoi), nous avons 6 combinaisons à explorer pour placer 2 voisins. On remarque :
En excluant toutes les situations où un blé voisin se trouve en diagonale (nous verrons plus tard pourquoi), nous avons 6 combinaisons à explorer pour placer 2 voisins. On remarque :
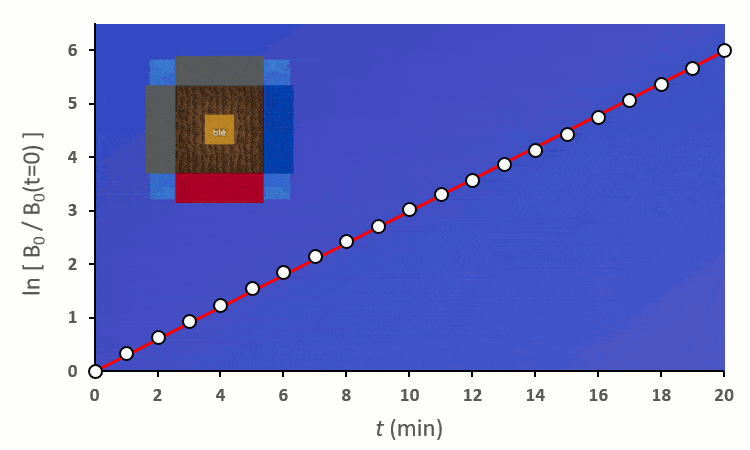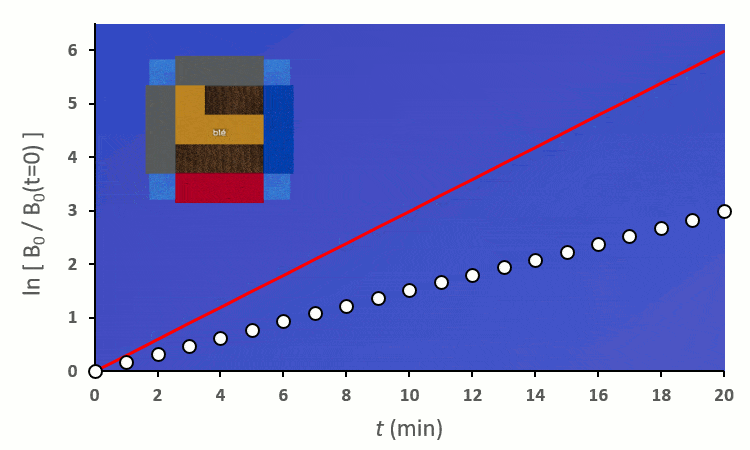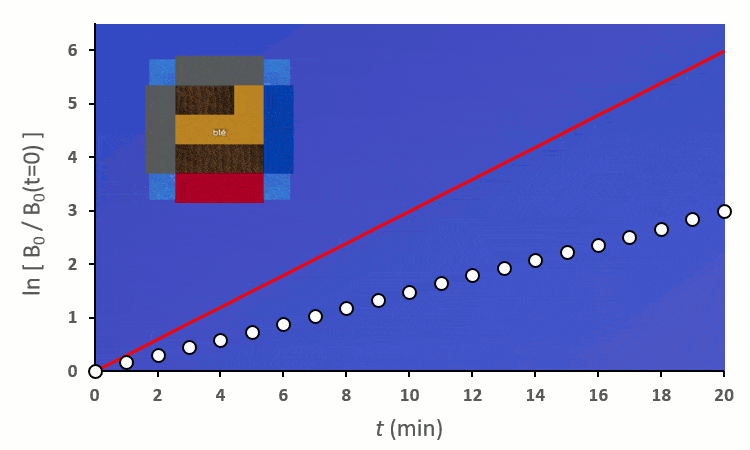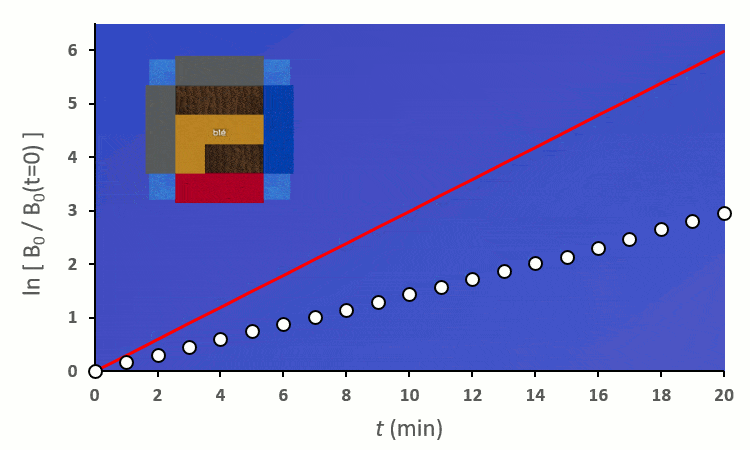 A partir de trois blés, on remarque rapidement que la constante de vitesse $k’_0$ est forcée de descendre :
A partir de trois blés, on remarque rapidement que la constante de vitesse $k’_0$ est forcée de descendre :
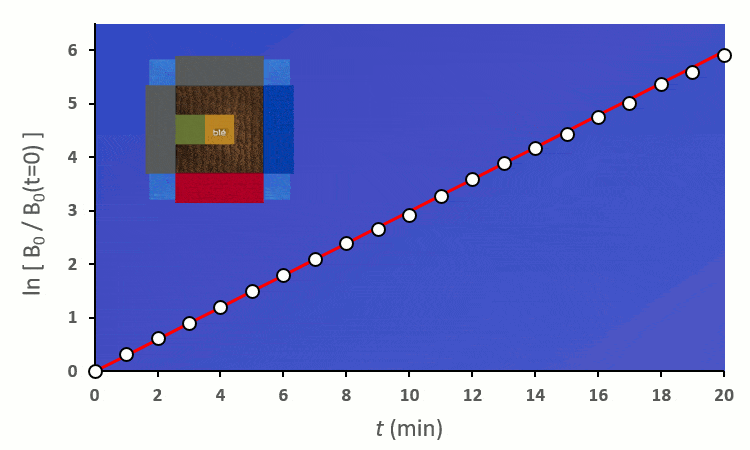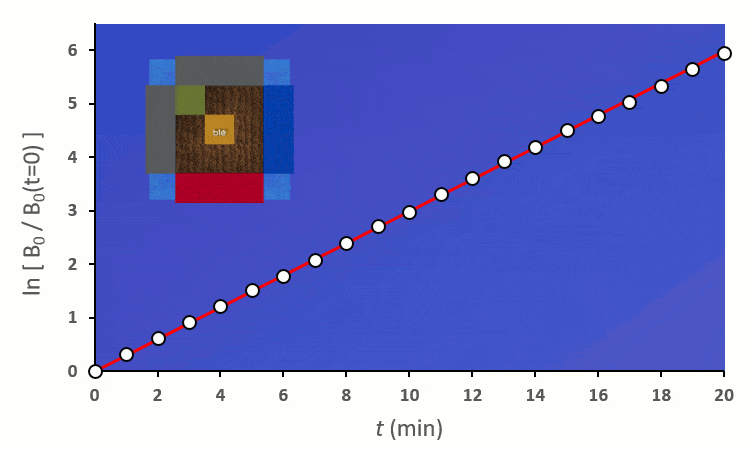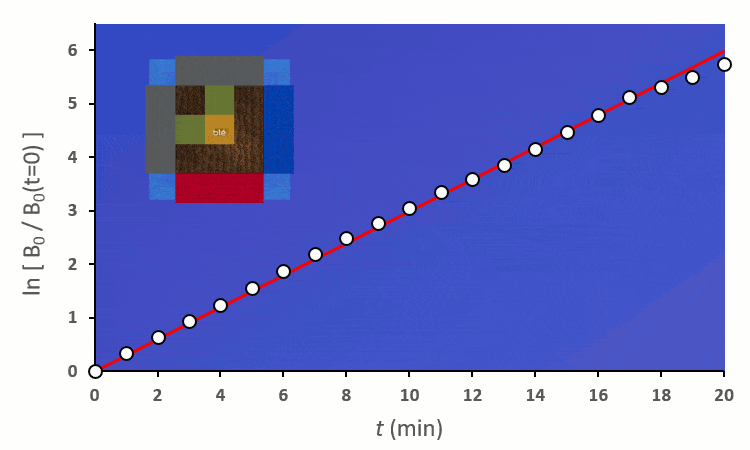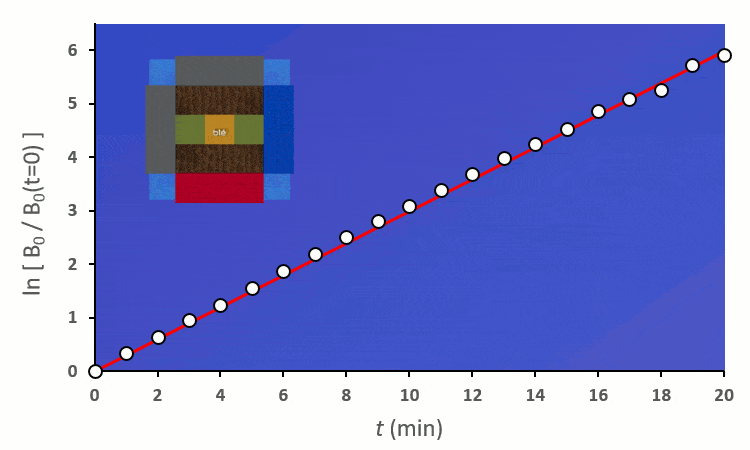 Recommençons nos expériences en remplaçant les blés voisins par des carottes (ici représenté en vert) : on remarque… aucun changement.
Recommençons nos expériences en remplaçant les blés voisins par des carottes (ici représenté en vert) : on remarque… aucun changement.
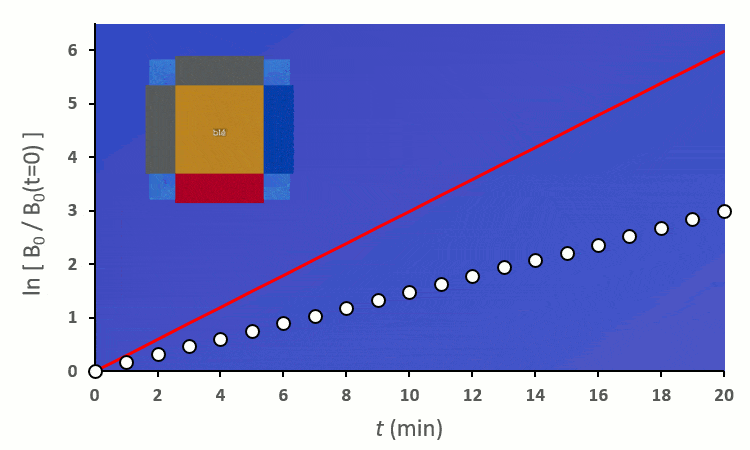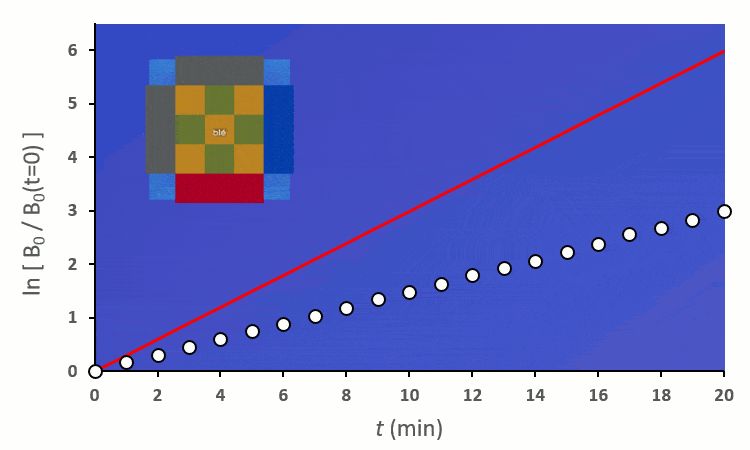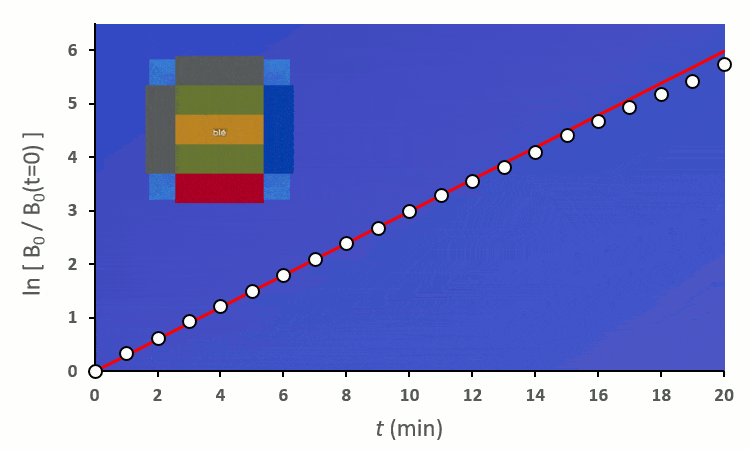 Ainsi, on peut confirmer les observations faites sur le terrain :
Ainsi, on peut confirmer les observations faites sur le terrain :
Conclusion :
Téléchargement :

![[TestZone] #5 – Agriculture : disposition & croissance](https://www.minecraft-france.fr/wp-content/uploads/2016/07/Une_testzone_5.jpg)
Excellent article d’une complexité inattendue. J’étais loin d’imaginer qu’il y avait d’autres facteurs que l’irrigation et la lumière à prendre en compte pour la culture du blé. C’est pourquoi je suis arrivé ici par hasard après être tombé sur “culture en bande” dans le Minecraft Wiki. Je pensais chaque bloc de culture indépendant…
Cet article est juste parfait. C’est juste excellent, continue, moi j’en veux plus!
J’ai enfin compris comment tout cela fonctionnait !
Merci pour cet excellent article, très complet ;)
Superbe ! Je pige rien aux formules mais on voit bien que le travail accompli est fou !
Ps : envoie ton article à Nature
Exellent, comme d’hab. J’espère que sa te servira un jour dans un CV ! =D
@cercus Et pourtant, c’est bien pratique que ce soit en chimie ou en physique. Je crois aussi que le programme de prépa MP/PC est toujours le même par contre et qu’ils mangent les équa diff du second degré dès la première année.
@cercus : En effet, c’est un changement assez récent. ^^
Et les profs de maths de S ont quand même tendance à enseigner les équa diffs de premier ordre en toute fin d’année.
“Il s’agit d’une équation différentielle du premier ordre, et sa résolution est au programme des terminales scientifiques. La forme générale des solutions est ”
-> Ce n’est plus au programme
Excellent boulot!
GG l’article est genial , super bien redige et tres professionnel juste bravo
Jé pa conpri l ékasion mais le reste j’ai trouvé ça génial .
GG à toi !
et bien c’est… comment dire… TRES complexe surtout au niveau des equation… je suis qu’en 3eme moi! mais n’enpeche cet article vas bien m’aider…
Très complet GG !
Très complet comme dossier, bien joué ;)